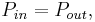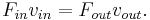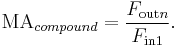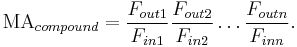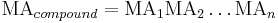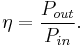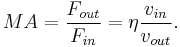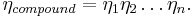Simple machine

A simple machine is a mechanical device that changes the direction or magnitude of a force. In general, they can be defined as the simplest mechanisms that provide mechanical advantage (also called leverage).[2]

Usually the term refers to the six classical simple machines which were defined by Renaissance scientists:[3]

These simple machines fall into two classes: (i) the inclined plane, wedge, screw characterized by the vector resolution of forces and movement along a line, and (ii) the lever, pulley, wheel and axle characterized by the equilibrium of torques and movement around a pivot.

A simple machine is an elementary device that has a specific movement (often called a mechanism), which can be combined with other devices and movements to form a machine. The view of machines as decomposable into simple machines arose in the Renaissance as an interpretation of Greek texts on technology.[4]

Simple machines are considered to be the "building blocks" of more complicated machines. For example, wheels, levers, and pulleys are all used in the mechanism of a bicycle.[5][6]

A page from a 1728 text by Ephraim Chambers[1] (see figure to the right) shows more simple machines. By the late 1800's Franz Reuleaux[7] identified hundreds of simple machines. Models of these devices can be found at Cornell's KMODDL site.

Contents

History

The idea of a "simple machine" originated with the Greek philosopher Archimedes around the 3rd century BC, who studied the "Archimedean" simple machines: lever, pulley, and screw.[2][8] He discovered the principle of mechanical advantage in the lever.[9] Later Greek philosophers defined the classic five simple machines (excluding the inclined plane) and were able to roughly calculate their mechanical advantage.[4] Heron of Alexandria (ca. 10–75 AD) in his work Mechanics lists five mechanisms that can "set a load in motion"; lever, windlass, pulley, wedge, and screw,[8] and describes their fabrication and uses.[10] However the Greeks' understanding was limited to the statics of simple machines; the balance of forces, and did not include dynamics; the tradeoff between force and distance, or the concept of work.

During the Renaissance the dynamics of the Mechanical Powers, as the simple machines were called, began to be studied from the standpoint of how much useful work they could perform, leading eventually to the new concept of mechanical work. In 1586 Flemish engineer Simon Stevin derived the mechanical advantage of the inclined plane, and it was included with the other simple machines. The complete dynamic theory of simple machines was worked out by Italian scientist Galileo Galilei in 1600 in Le Meccaniche ("On Mechanics").[11][12] He was the first to understand that simple machines do not create energy, only transform it.[11]

The classic rules of sliding friction in machines were discovered by Leonardo Da Vinci (1452–1519), but remained unpublished in his notebooks. They were rediscovered by Guillaume Amontons (1699) and were further developed by Charles-Augustin de Coulomb (1785).[13]

Mechanical advantage

A simple machine has an applied force that works against a load force. If there are no friction losses, the work done on the load is equal to the work done by the applied force. This allows an increase in the output force at the cost of a proportional decrease in the distance moved by the load. The ratio of the output force to the input force is the mechanical advantage of the machine.

If the simple machine does not dissipate or absorb energy, then its mechanical advantage can be calculated from the machine's geometry. For example, the mechanical advantage of a lever is equal to the ratio of its lever arms. A simple machine with no friction or elasticity is often called an ideal machine.[14][15]

In an ideal simple machine, the rate of energy in, or power in, equals the rate of energy out, or power out. Power is defined as the force multiplied by the velocity of its point of application. So the applied force times the velocity the input point moves, 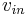v_{in}\,, must be equal to the load force times the velocity the load moves, v_{out}\,:

P_{in} = P_{out}, \!

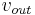or

F_{in}v_{in} = F_{out}v_{out}.\,

So the ratio of output to input force, the mechanical advantage, of a frictionless machine is equal to the "velocity ratio"; the ratio of input velocity to output velocity:

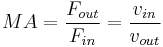MA = \frac{F_{out}}{F_{in}} = \frac{v_{in}}{v_{out}} \,      (Ideal Mechanical Advantage)

In the screw, which uses rotational motion, the input force should be replaced by the torque, and the velocity by the angular velocity the shaft is turned.

Compound machine

A compound machine is a machine formed from a set of simple machines connected in series with the output force of one providing the input force to the next. For example a bench vise consists of a lever (the vise's handle) in series with a screw, and a simple gear train consists of a number of gears (wheels and axles) connected in series.

The mechanical advantage of a compound machine is the ratio of the output force exerted by the last machine in the series divided by the input force applied to the first machine, that is

\mathrm{MA}_{compound} = \frac {F_{\mathrm{out} n}} {F_{\mathrm{in} 1}}. \,

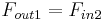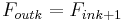Because the output force of each machine is the input of the next, F_{out 1}=F_{in 2} \, and F_{out k} =F_{in k%2B1} \,, this mechanical advantage is also given by,

\mathrm{MA}_{compound} = \frac {F_{out 1}} {F_{in 1}} \frac {F_{out 2}} {F_{in 2}} \ldots\frac {F_{out n}} {F_{in n}}. \,

Thus, the mechanical advantage of the compound machine is equal to the product of the mechanical advantages of the series of simple machines that form it,

\mathrm{MA}_{compound} = \mathrm{MA}_1 \mathrm{MA}_2 \ldots\mathrm{MA}_n \,

Energy losses and efficiency

Machines lose energy through friction, deformation and wear, which is dissipated as heat. This means the power out of the machine is less than power in. The ratio of power out to power in is the efficiency η of the machine, and is a measure of the energy losses,

\eta = \frac{P_{out}}{P_{in}}. \,

The velocity ratio of a machine is fixed by its dimensions, so it is the mechanical advantage that is reduced by the losses, that is

MA = \frac{F_{out}}{F_{in}} = \eta \frac{v_{in}}{v_{out}}.

So in non-ideal machines, the mechanical advantage is always less than the velocity ratio by the product with the efficiency η. So a machine that includes losses such as friction, deformation and wear, will not be able to move as large a load as a corresponding ideal machine using the same input force.

The efficiency of a compound machine is the product of the efficiencies of the series of simple machines that form it,

\eta_{compound} = \eta_1 \eta_2 \ldots \eta_n.\,

See also

References

  1. ^ a b Table of Mechanicks, from Ephraim Chambers (1728) Cyclopaedia, A Useful Dictionary of Arts and Sciences, Vol. 2, London, p.528, Plate 11.
  2. ^ a b Asimov, Isaac (1988). Understanding Physics. New York: Barnes & Noble. p. 88. ISBN 0880292512. http://books.google.com/books?id=pSKvaLV6zkcC&pg=PA88&dq=Asimov+simple+machine&cd=1#v=onepage&q&f=false. 
  3. ^ Anderson, William Ballantyne (1914). Physics for Technical Students: Mechanics and Heat. New York, USA: McGraw Hill. pp. 112–122. http://books.google.com/books?id=Pa0IAAAAIAAJ&pg=PA112. Retrieved 2008-05-11. 
  4. ^ a b Usher, Abbott Payson (1988). A History of Mechanical Inventions. USA: Courier Dover Publications. pp. 98. ISBN 048625593X. http://books.google.com/books?id=xuDDqqa8FlwC&pg=PA196#v=snippet&q=wedge%20and%20screw&f=false. 
  5. ^ Prater, Edward L. (1994), Basic Machines, Naval Education and Training Professional Development and Technology Center, NAVEDTRA 14037
  6. ^ Bureau of Naval Personnel, 1971, Basic Machines and How They Work, Dover Publications.
  7. ^ Reuleaux, F., 1876 'The Kinematics of Machinery,' (trans. and annotated by A. B. W. Kennedy), reprinted by Dover, New York (1963)
  8. ^ a b Chiu, Y.C. Chiu (2010). An introduction to the History of Project Management. Delft: Eburon Academic Publishers. pp. 42. ISBN 9059724372. http://books.google.com/books?id=osNrPO3ivZoC&pg=PA42&dq=%22heron+of+alexandria%22++load+motion#v=onepage&q=%22heron%20of%20alexandria%22%20%20load%20motion&f=false. 
  9. ^ Ostdiek, Vern; Bord, Donald (2005). Inquiry into Physics. Thompson Brooks/Cole. p. 123. ISBN 0534491685. http://books.google.com/books?id=7kz2pd14hPUC&pg=PA123. Retrieved 2008-05-22. 
  10. ^ Strizhak, Viktor; Igor Penkov, Toivo Pappel (2004). "Evolution of design, use, and strength calculations of screw threads and threaded joints". HMM2004 International Symposium on History of Machines and Mechanisms. Kluwer Academic publishers. p. 245. ISBN 1402022034. http://books.google.com/books?id=FqZvlMnjqY0C&printsec=frontcover&dq=%22archimedean+simple+machine%22&source=gbs_summary_r&cad=0. Retrieved 2008-05-21. 
  11. ^ a b Krebs, Robert E. (2004). Groundbreaking Experiments, Inventions, and Discoveries of the Middle Ages. Greenwood Publishing Group. p. 163. ISBN 0313324336. http://books.google.com/books?id=MTXdplfiz-cC&pg=PA163&dq=%22mechanics+Galileo+analyzed%22#v=onepage&q=%22mechanics%20Galileo%20analyzed%22&f=false. Retrieved 2008-05-21. 
  12. ^ Stephen, Donald; Lowell Cardwell (2001). Wheels, clocks, and rockets: a history of technology. USA: W. W. Norton & Company. pp. 85–87. ISBN 0393321754. http://books.google.com/books?id=BSfpFLV1nkAC&pg=PA86&dq=%22simple+machine%22+galileo#v=onepage&q=%22simple%20machine%22%20galileo&f=false. 
  13. ^ Armstrong-Hélouvry, Brian (1991). Control of machines with friction. USA: Springer. pp. 10. ISBN 0792391330. http://books.google.com/books?id=0zk_zI3xACgC&pg=PA10&dq=friction+leonardo+da+vinci+amontons+coulomb#v=onepage&q=friction%20leonardo%20da%20vinci%20amontons%20coulomb&f=false. 
  14. ^ J. J. Uicker, G. R. Pennock, and J. E. Shigley, 2003, Theory of Machines and Mechanisms, Oxford University Press, New York.
  15. ^ B. Paul, 1979, Kinematics and Dynamics of Planar Machinery, Prentice Hall.